Vamos aprender a sumar y restar vectores, por el método gráfico, el analítico y el método de descomposición con ejercicios resueltos y explicados.
Antes de empezar, si quieres repasar la teoría de vectores te recomendamos el siguiente enlace: Vectores
Suma de Vectores
Para sumar dos vectores de forma gráfica solo hay que poner uno detrás de otro y unir el principio del primero con el final del segundo.
Mira el ejemplo:
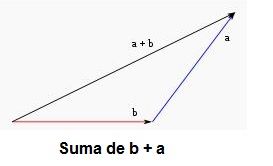
Vamos a sumar dos vectores, el a y el b.
Fíjate que desde el final del vector a trazamos una paralela de igual tamaño que el vector b.
El inicio de a y el final de la paralela trazada será el vector suma de los dos iniciales.
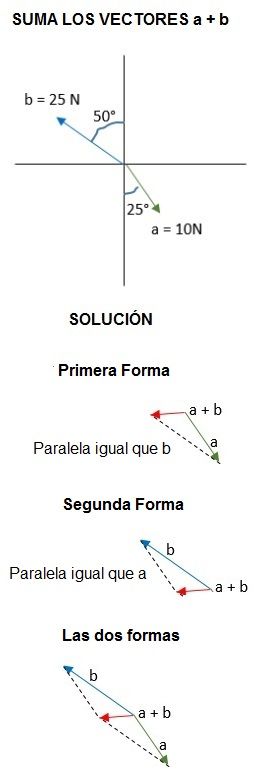
También podemos hacerlo desde el final de b trazando una paralela del vector a.
El resultado será el mismo de una u otra forma. El vector rojo es la suma.
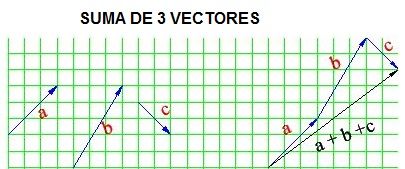
Para sumar 3 vectores (o la cantidad que sea) solo hay que poner uno detrás del otro y unir el principio del primero con el final del último.Veamos un ejemplo:
Suma de Vectores de Forma Analítica
El primer caso es que nos den los puntos de las coordenadas de los dos vectores.
En este caso es muy fácil, solo hay que sumar las coordenadasen X de los dos vectores y las coordenadas en Y.
El resultado es el vector suma. Veamos un ejercicio:
Tenemos las coordenadas del vector A que son ( – 3, 4) y la del vector B que son (4,2).
¿Cual será el vector suma de los dos?
el vector AB = (-3 + 2) (4 + 2) = (1, 6) Hemos obtenido las coordenadas del vector suma de los dos anteriores el A y el B.AB = (1, 6)
Suma de Vectores por Descomposición
El segundo caso, es que nos den el valor del módulo del vector y un ángulo.
Para sumar dos vectores hay que sumar los componentes X de cadavector y los Y, pero no las conocemos directamente.
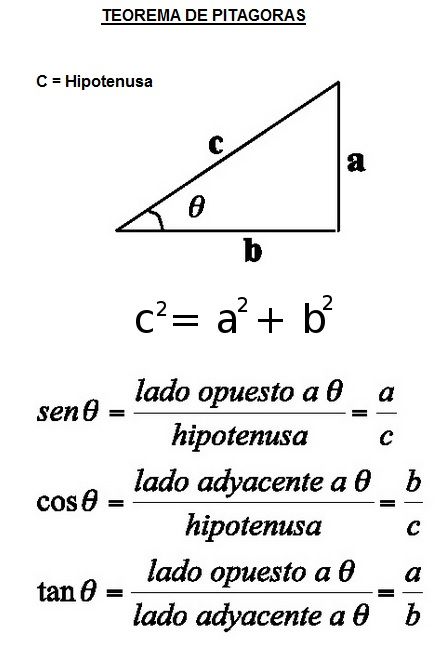
Lo primero que tenemos que saber es el teorema de Pitágoras para descomponer el vector.
El teorema de Pitágoras es para resolver triángulos, date cuenta que si descomponemos un vector es sus dos componentes X e Y lo que tenemos es un triángulo, por eso aplicamos el teorema de Pitágoras.
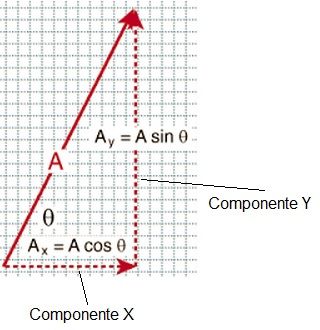
el vector A se descompone de la siguiente forma A = Ax + Ay; aveces lo verás expresado de esta otra forma A = Axi + Ayj , pero es lo mismo, la componente i es la X y la j la Y. la i y la j son vectores que se llaman vectores unitarios, son vectores que valen 1, en la dirección X (eli) y en la dirección Y (el j)
No te líes que es muy fácil.
Mira el teorema de Pitágoras y fíjate por qué Ax = A por el coseno θ y Ay = A por el seno θ.
Según el teorema tenemos que : Fx = F x cos θ y la Fy =F x cos θ.
Ya estamos preparados para hacer algún ejercicio. Solo tienes que descomponer las componentes X (o Y) de todos los vectores y sumarlas, luego haz lo mismo con las componentes Y (o j). El resultado será el vector suma.
Suma de Vectores Ejercicios Resueltos
Sumar el siguiente sistema de vectores a y b y obtener la resultante gráfica y analítica.
Vector a módulo de 5
Vector b módulo de 3
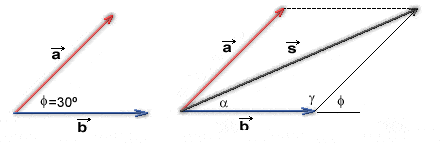
La solución Gráfica sería:
Descomponemos los vectores:
ax = a x coseno 30 = 5 x 0.86 = 4,33
ay = a x seno 30 = 5 x 0,5 = 2,5
bx = 3; solo tiene componente X, no tiene Y.
El vector suma será s = (ax + bx) (ay+ by) = (4,33 + 3) ( 2,5 + 0) = (7.33, 2,5) También podríamos verlo expresado de esta forma s = 7,33j + 2,5i
Estas coordenadas son los componentes X e Y del nuevo vector.
Si queremos saber su módulo, aplicando Pitágoras será la hipotenusa de ab, o lo que es lo mismo raíz cuadrada del cuadrado de 7,33 + el cuadrado de 2,5.
7,332 + 2,52= 53,72 + 6,25 = 59,67 ===> la raíz será √59,67 = 7,74 que será el módulo de s
Como s y sus componentes forman también un triangulo, calculemos el ángulo que forma por Pitágoras
El ángulo que forma será : coseno ∝ = Sx / S ==> coseno ∝ = 7,33/7,74 = 0,9470
El arco coseno es el ángulo de un coseno. Con una calculadora científica calculamos el arcoseno de 0,9470 y nos dará el ángulo que forma ese coseno. En nuestro caso arcoseno (0,9470) = 18.73 Grados. Este será el ángulo que forma s con la horizontal ∝ (eje X).
Problema Resuelto. Veamos otro ejercicio:
Ejercicio Suma de Vectores
Encuentra en forma analítica las componentes rectangulares de un vector cuyo módulo es de 60 y forma un ángulo de 45º con respecto a la horizontal en sentido noreste.
Datos
α = 450
sen 450= 0.7
cos 450= 0.7
ax ≈ ?
coseno 45º = ax/a; seno 45º = ay/a ==> Despejando las componentes será:
ax= a cos 450
ay= a sen 450
Sustituimos y calculamos
ax= 60 cos 450 = 60∙0.7= 42
ax= 42
ay= 60 sen450 = 60∙0.7= 42
ay= 42
Las dos componentes tendrán el mismo valor. Problema Resuelto.
¿Todavía no lo tienes claro?
Veamos otro explicado en el siguiente vídeo:
En el siguiente enlace tienes un ejercicio de suma de 3 vectores: Suma de 3 Vectores
Resta de Vectores
Resta de Vectores Método Gráfico
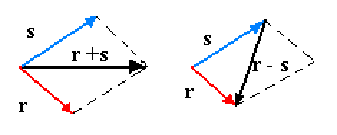
La resta es exactamente igual que la suma solo que en lugar de sumar tendremos que restar las componentes. En el caso del método gráfico tendremos que restar los vectores también. Es muy fácil, solo hay que unirlos dos vectores por su principio y unir los finales. Fíjate en el siguiente ejemplo, primero sumamos y luego restamos:
Resta de Vectores por Método Analítico
Si nos dan las componentes (forma analítica) de los vectores, tendríamos que restar las componentes x y las componentes y.
Ejercicio Resta de Vectores
Tenemos las coordenadas del vector A que son ( – 3, 4) y la del vector B que son (4,2). ¿Cual será el vector resta de los dos?
el vector AB = (-3 – 2) (4 – 2) = (-5, 2) Hemos obtenido las coordenadas del vector suma de los dos anteriores el A y el B.AB = (-5, 2)
Por el método de descomposición tendríamos que calcular sus componentes y después restarlas. Para eso, como en la suma, aplicamos Pitágoras.
Veamos un ejercicios y su solución en el siguiente vídeo:
Aqui te dejamos algunos ejercicios de vectores resueltos:
En este otro enlace tienes más ejercicios sobre vectores: Ejercicios Vectores
Si te ha gustado pulsa en Compartir. Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.

Me interesa la clase