Vamos a explicar el movimiento de caída libre de los cuerpos.
También te recomendamos que veas el vídeo de la parte de abajo para entender bien las Fórmulas de caída libre de física.
Para entender como se resuelven este tipo de problemas y como usar las fórmulas, lo mejor es hacerlo resolviendo problemas de caída libre.
Primero veremos las fórmulas y luego algunos problemas con las soluciones y explicados.
Si quieres ver más ejercicios resueltos: Ejercicios de Caída Libre.
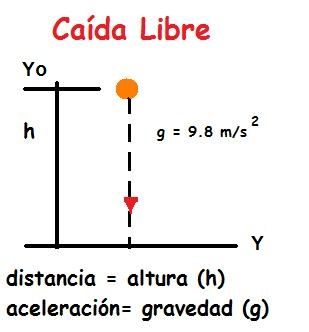
El movimiento vertical de cualquier objeto en movimiento libre (Caída libre), se puede calcular mediante las formulas de caída libre que son las siguientes.
Indice de Contenidos
Formulas de Caída Libre
Fórmulas del Movimiento de Caída Libre
a). V = Vo +- gt Si el cuerpo está cayendo se suma el producto gt = gravedad x tiempo.
Si el cuerpo sube se resta el producto gt.
¿Por qué?.
Muy sencillo, piensa que si el objeto está cayendo, la fuerza de gravedad (g) hace que aumente cada vez más su velocidad, lo que hace que la velocidad final V sea mayor, por eso se pone +. V =Vo + gt. (la velocidad va aumentando)
Si el objeto sube, la gravedad actúa en su contra disminuyendo la velocidad del objeto, en este caso será el signo -, ya que la velocidad del objeto con el paso del tiempo irá disminuyendo. V = Vo – gt (la velocidad va disminuyendo)
Luego el signo de la gravedad depende si el cuerpo sube o baja. En caída libre siempre será + en la velocidad.
Ahora veamos la de la distancia recorrida por el objeto.
E = Eo + Vo * t – 1/2 gt² Aquí pondremos el signo – por que si soltamos el objeto desde una altura, la gravedad hará que recorra menos espacio, en el mismo tiempo, porqué la gravedad en el caso de caída acelera el cuerpo.
Pero además en caída libre E (espacio recorrido por el cuerpo) será la altura desde donde soltamos el cuerpo, hasta llegar al suelo, donde la altura será cero.
Según lo dicho podemos transformar la fórmula para caída libre a la siguiente fórmula.
b). Y = vo t + Yo – 0.5 gt² (Recuerda que 0.5 = 1/2)
Ojo si el objeto lo soltamos desde una altura, su Vo = 0 y la altura final (el suelo) será Y = 0.
Otra fórmula es:
c). V² = Vo² – 2g( Y – Yo)
Esta fórmula la usaremos cuando no nos dan el tiempo, fíjate que no aparece el tiempo por ningún lado en la fórmula.
Resumen: V es velocidad final, g la gravedad (en la tierra 9,8m/s, se puede aproximar a 10), Vo velocidad inicial, Vm velocidad media, t es el tiempo, la y es la altura final (si cae en el suelo será cero), la Yo es la altura inicial desde donde se suelta el objeto.
Ojo en algunos libros veremos como a las Y se les llama h o altura.
Las Ecuaciones Dinámicas en Caída libre son las siguientes:
V² = Vo² – 2g( Y – Yo)
Y = Yo + Vo t – ½ g t²
V = Vo – g t
Y – Yo = ½ (V + Vo) t
Ahora te toca practicar a tí.
Resolver los siguientes problemas:
En todos los casos usar g = 10 m/s ².
Problema n° 1)
Desde el balcón de un edificio se deja caer una manzana y llega a la planta baja en 5 s.
a) ¿Desde qué piso se dejo caer, si cada piso mide 2,88 m?.
b) ¿Con qué velocidad llega a la planta baja?.
Respuestas:
a) 43
b) 50 m/s
Problema n° 2)
Si se deja caer una piedra desde la terraza de un edificio y se observa que tarda 6 s en llegar al suelo. Calcular:
a) A qué altura estaría esa terraza.
b) Con qué velocidad llegaría la piedra al piso.
Respuestas:
a) 180 m
b) 60 m/s
Problema n° 3)
¿De qué altura cae un cuerpo que tarda 4 s en llegar al suelo?.
Respuesta: 80 m
Problema n° 4) Un cuerpo cae libremente desde un avión que viaja a 1,96 km de altura, cuánto tarda en llegar al suelo?.
Respuesta: 19,8 s
Aclaración: Si dejamos caer una pelota de madera y una hoja de papel, al mismo tiempo y de la misma altura, observaremos que la pelota llega primero al suelo.
Pero, si arrugamos la hoja de papel y realizamos de nuevo el experimento observaremos que los tiempos de caída son casi iguales.
Esto es por que la hoja tiene menos superficie. Si quieres saber más sobre esto te recomendamos este enlace Caída de los Cuerpos.
Sistemas de Referencia
Además de las ecuaciones de cinemática, hay que considerar algo muy importante en los ejercicios de caída Libre, y es; la ubicación del Sistema Referencial o inercial, ya que a partir de allí dependerán los signos y los valores de “Y” y “Yo”.
Los signos se considerarán negativos si realizamos las mediciones hacia abajo. Veamos ejemplos para aclararnos.
Ejemplo N º 1
Supongamos que un objeto se deja caer desde la parte superior de una torre:
CASO I
Ubicamos el sistema referencial en el piso.
“Yo”: es igual a la altura de la torre
“Y”: es cero; ya que es el momento cuando toca el piso.
CASO II
Ubicamos el sistema referencial en la parte superior de la Torre.
“Y”: es igual a la altura de la torre, (es el momento cuando el objeto toca el piso, pero con signo negativo).
Para ese instante la velocidad del objeto vale cero.
“Yo”: es igual a cero; (es el punto de partida)
Ejemplo N º 2
Supongamos que un objeto se lanza verticalmente hacia arriba, desde la parte superior de una torre:
CASO I
Ubicamos el sistema referencial en el piso.
“Yo”: es igual a la altura de la torre
“Y” : es la altura máxima que alcanza el objeto, medido desde el punto de partida, (pero en el resultado hay que tener en cuanta la altura de la torre mas lo que sube el objeto producto de la fuerza que se le impuso al lanzarlo)
Para ese instante la velocidad del objeto vale cero.
“Y” será igual a la altura de la torre, pero con signo negativo; cuando se pregunta por el tiempo que tarda en tocar el piso o la velocidad al llegar al piso.
CASO II
Ubicamos el sistema referencial en la parte superior de la Torre.
“Yo”: es igual a cero
“Y” : es la altura máxima que alcanza el objeto, medido desde el punto de partida, (pero para el resultado hay que tener en cuenta la altura de la torre mas lo que sube el objeto producto de la fuerza que se le impuso al lanzarlo)
Para ese instante la velocidad del objeto vale cero.
“Y” será igual a la altura de la torre, pero con signo negativo, cuando se pregunta por el tiempo que tarda en tocar el piso o la velocidad al llegar a este.
Si quieres ver más problemas resueltos visita el siguiente enlace: Ejercicios de Caida Libre.
Vídeo Explicando el Movimiento
Aquí te dejamos un video que explica el movimiento bastante bien, por si todavía tienes dudas.
Ejercicios de Caída Libre Resueltos
Para ver más ejercicios resueltos y explicados visita: Ejercicios de Caída Libre
Si te ha gustado pulsa en Me gusta. Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
quien es el autor para poder referenciar en APA
La referencia es la URL es decir, http://www.areaciencias.com y el autor Ernesto Rodriguez. Un saludo
Quien es el autor y cual es la referencia en apa
La referencia es la URL es decir, http://www.areaciencias.com y el autor Ernesto Rodriguez. Un saludo