Los proyectiles son objetos lanzados que están sujetos solo al efecto de la gravedad, lo que significa que el objeto se mueve horizontal y verticalmente simultáneamente.
El resultado de una fuerza vertical que actúa sobre un objeto en movimiento horizontal es hacer que el objeto se desvíe de su trayectoria lineal.
Este tipo de movimiento se llama movimiento o tiro parabólico.
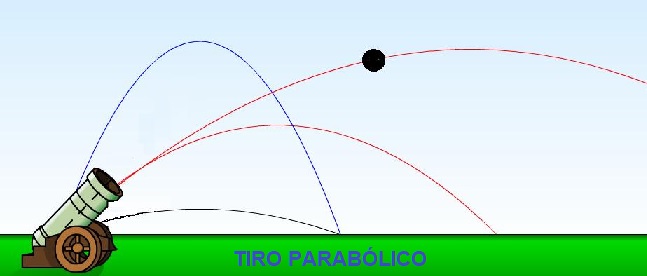
Por ejemplo una pelota de golf golpeada por un jugador también sigue el movimiento del proyectil, la pelota se mueve horizontalmente con el objetivo de llegar al hoyo mientras se mueve hacia arriba y luego hacia abajo debido a la acción de la gravedad.
Indice de Contenidos
Características del Tiro Parabólico
El movimiento del proyectil se divide en dos movimientos, horizontal y vertical, y son completamente independientes entre sí.
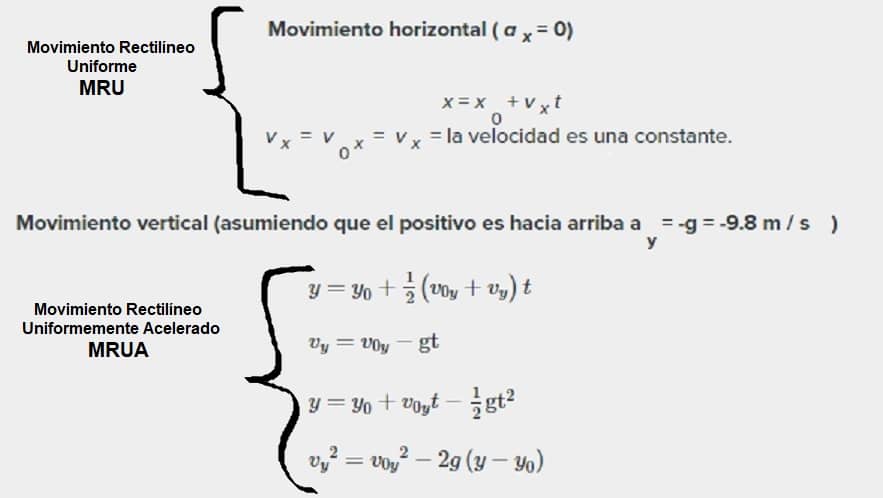
-En el movimiento horizontal, el proyectil se mueve a una velocidad constante, como en el movimiento rectilíneo uniforme (MRU).
-En el movimiento vertical, el objeto se mueve de acuerdo con la aceleración gravitacional y por lo tanto, actúa como un cuerpo en caída libre, o lo que es lo mismo, con movimiento rectilíneo uniformemente acelerado (MRUA).
-No se tiene en cuenta el rozamiento del aire, de lo contrario no sería MRUA.
Luego, más abajo, veremos las fórmulas de los 2 movimientos.
-Los valores de velocidad obtenidos al inicio son los mismos que los valores cuando el proyectil golpea el suelo.
–En el punto más alto, la velocidad vertical es cero y por tanto el objeto solo tiene un componente de velocidad horizontal.
Vy = 0
–El movimiento del proyectil es simétrico y el punto de simetría se ubica cuando el proyectil alcanza su punto más alto.
Un proyectil lanzado desde el suelo siempre cae al suelo, al final de su movimiento, con velocidades idénticas a las que tenía al inicio (asumiendo que el suelo al final del movimiento no es ni más alto ni más bajo que el suelo en el inicio), porque el movimiento del proyectil es simétrico en su punto medio.
-El tiempo que tarda el proyectil en alcanzar el punto más alto es igual al tiempo que tarda ese mismo proyectil en volver al suelo desde la altura máxima.
–Inicialmente la velocidad es positiva, porque el movimiento está orientado hacia arriba, pero al final, la velocidad es negativa, porque el movimiento está orientado hacia el suelo.
Pasos Para la Resolución de Problemas
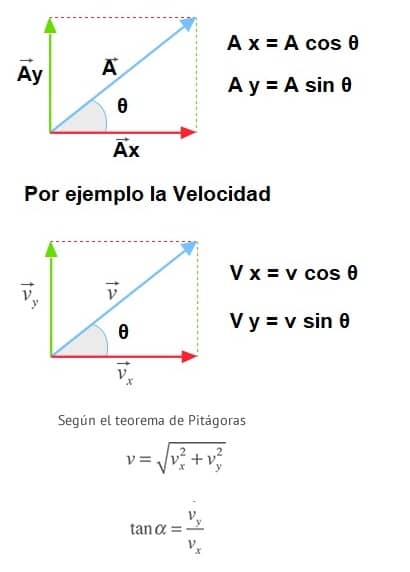
1º) Divide el movimiento en 2 componentes, horizontales y verticales a lo largo de los ejes X e Y.
Estos ejes son perpendiculares, por lo que el valor de cada componente será
La componente X : A x = A cos θ
Y la componente Y : A y = A sin θ
Por ejemplo, las magnitudes de las componentes de la velocidad v serán:
V x = v cos θ
V y = v sin θ
Donde v es la magnitud de la velocidad y θ es su dirección
Los valores iniciales se indican con un subíndice 0 (cero), como de costumbre.
Y0, X0, Vox e Voy.
Lo mismo ocurrirá con las componentes del desplazamiento del proyectil (s), como luego veremos.
2º) Tienes que resolver el movimiento como dos movimientos unidimensionales independientes, uno horizontal y otro vertical.
Las ecuaciones para el movimiento horizontal y vertical serán:
3º) Resuelve las incógnitas en los dos movimientos separados: uno horizontal y otro vertical.
Ten en cuenta que la única variable común entre los movimientos es el tiempo t .
4º) Por último r tenemos que recombinar los dos movimientos para encontrar el desplazamiento total s y la velocidad v.
El desplazamiento total S será la hipotenusa de los 2 movimientos, el horizontal en el eje X y el vertical en el eje Y, por lo que por trigonometría será la raíz cuadrada de los 2 componentes al cuadrado:
Lo mismo para la velocidad total:
Tiempo de Vuelo
El proyectil volará hasta que la Y sea igual a 0.
Alcance Máximo
Es la distancia en horizontal que recorre el proyectil.
Podemos obtenerlo si sustituimos en la ecuación de la coordenada X el tiempo de vuelo.
Altura Máxima
Será cuando Vy = 0
Es decir Voy – gt = 0
Podemos ver aquí todas las fórmulas utilizadas.
Tiro Parabólico Formulas
Veamos algunos ejercicios:
Ejercicios Tiro Parabólico
1)Un futbolista chuta un balón desde el césped a una velocidad de 26 m/s.
Si el balón sale del suelo con un ángulo de 40° y cae sobre el campo sin que antes lo toque ningún jugador, calcular:
a) La altura máxima del balón
b) La distancia desde el portero hasta el punto donde caerá en el campo
c) El tiempo en que la pelota estará en el aire
2) Un arquero dispara una flecha cuya velocidad de salida es de 100m/s y forma un ángulo de 30º
con la horizontal. Calcula:
a) El tiempo que la flecha está en el aire.
b) La altura máxima.
c) El alcance máximo.
d) La velocidad a lo 4 segundos.
e) La velocidad final.
3) Desde la parte superior de un edificio de 4,9 metros de altura se lanza horizontalmente una pelota de básquet y cae al suelo en un punto situado a 7 metros del borde del edificio. Hallar la velocidad de la pelota en el instante en que fue lanzada. Usar g = 9,8 m/s2.
Si te ha gustado la página sobre el Tiro Parabólico pulsa en Compartir. Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
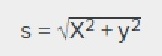








Gracias me ayudó con la tarea 💖
hola gracias es de gran ayuda